Um simples tutorial para ensinar uma forma de resolver um cubo mágico 3×3. Será demonstrado uma das resoluções mais famosas, reconhecida por: Camadas, Cruzes, Fridrich, CFOP, entre outros nomes. Tal resolução consiste em resolver cada camada do cubo sequencialmente, metodologia idealizada por Jessica Fridrich e aprimorada durante muitos anos.
Resumo das fórmulas:
Montar a cruz branca (Usando lógica)
Montar diagonais da cruz branca (Também pela lógica)
Ajustar segunda camada (Esquerda)
Ajustar segunda camada (Direita)
Criar cruz amarela
Ajustar as cores das laterais da cruz amarela
Posicionar as diagonais da face amarela no local correto
Orientar diagonais e finalizar o cubo
Introdução
Existem vários outros métodos e adaptações para resolver um cubo mágico, como Roux e ZZ, além de várias estratégias mais avançadas para acelerar, ou até mesmo pular, certas etapas do método de Fridrich. Este artigo não abordará esses assuntos e ficará apenas no método básico da resolução por camadas.
Para gerar a maioria das imagens deste artigo, será usado o app online de cubo https://cube-solver.com/, uma ferramenta bem útil para ilustrar e resolver diferentes cubos, mas recomenda-se ter um cubo físico e de uso pessoal para melhor aprender sua resolução.
Lembre-se de se familiarizar com o cubo e seus movimentos antes de sair resolvendo. Entender onde certas peças estão indo em cada movimento é bem importante.
Sobre o Cubo Mágico em si
O mais famoso cubo mágico, 3×3, idealizado por Ernő Rubik em 1974, significa que em todas as suas direções (x,y,z) terão 3 peças. Por padrão, as faces de tal cubo sempre devem estar opostas à uma cor específica.
Posição das cores do cubo:
- Azul sempre vai estar oposto ao Verde
- Vermelho sempre vai ser oposto ao Laranja
- Amarelo sempre vai estar oposto ao Branco
É bem comum vários cubos de empresas diferentes acabarem saindo com as faces trocadas, ou o posicionamento delas invertido. Muitos acabam trocando o azul e verde de lugar, mas normalmente seguem o formato abaixo:
Conceitos utilizados no artigo
As imagens da seção de ‘Conceitos utilizados no artigo’ foram retiradas do site https://jperm.net/3×3/moves, local que também ensina os diferentes movimentos e expande em mais anotações.
Existem diversas fórmulas para a resolução de um cubo mágico, normalmente seguindo conotações inicialmente difíceis de entender. Para simplificar o processo ao leitor, serão utilizados termos mais simples, mas a anotação oficial também será apresentada. Segue um glossário dos movimentos mais comuns de um cubo 3×3:
| Forma oficial | Forma literal | Movimento |
| U | Topo -> Esquerda | |
| D | Base -> Direita | |
| R | Lateral Direita -> Cima | |
| L | Lateral Esquerda -> Baixo | |
| F | Frente -> Direita | |
| B | Costas -> Esquerda | |
| U’ | Topo -> Direita | |
| D’ | Base -> Esquerda | |
| R’ | Lateral Direita -> Baixo | |
| L’ | Lateral Esquerda -> Cima | |
| F’ | Frente -> Esquerda | |
| B’ | Costas -> Direita | |
| U2 | Topo -> Esquerda x2 | |
| D2 | Base -> Direita x2 | |
| R2 | Lateral Direita -> Cima x2 | |
| L2 | Lateral Esquerda -> Cima x2 | |
| F2 | Frente -> Direita x2 | |
| B2 | Costas -> Esquerda x2 |
Montando o cubo
Obs: Para as imagens abaixo, será utilizado o site https://cube-solver.com/, com apoio a algumas imagens auxiliares já prontas do site https://jperm.net/3×3.
Um embaralhamento especifico foi criado apenas para auxiliar na visualização.
Embora existam sites capazes de resolver o cubo automaticamente, eles não serão usados com essa finalidade neste artigo, servindo apenas para ilustrar cada cenário.
A lógica e metodologia ensinada abaixo é derivada do método Fridrich e demonstra a ilustração por trás de cada movimento:
O cubo embaralhado:
- Aprender a resolver um cubo mágico não necessita uma configuração específica. Utilize qualquer cubo 3×3 embaralhado e siga as instruções a seguir.
- Para embaralhar o cubo e facilitar um leitor acompanhando com um cubo real, uma formula especifica será apresentada, cabe ao leitor decidir seguir com ela ou não, as regras pode ser aplicada para qualquer cubo mágico 3×3 embaralhado.
- Imagem e formula exemplo para embaralhar um cubo:
- Com um cubo montado, a face branca virada para você e a face azul virada para cima, execute:

| Oficial | Literal |
| R | Lateral Direita -> Cima |
| U | Topo -> Esquerda |
| L | Lateral Esquerda -> Baixo |
| D | Base -> Direita |
| R | Lateral Direita -> Cima |
| U | Topo -> Esquerda |
| L | Lateral Esquerda -> Baixo |
| D | Base -> Direita |
* Lembrando, a formula acima não faz parte do algoritmo. Serve apenas para ilustrar um cubo embaralhado neste exemplo e permitir o leitor acompanhar a montagem.
- Resultado final após embaralhar um cubo embaralhado com a formula acima

Posicionamento e Primeiros passos:
Tente manter a mesma posição.
Evite fazer movimentos de girar o cubo enquanto está aprendendo a montar para não confundir o local das peças. De padrão, a maioria dos tutoriais ensina começando pela face branca, este post seguirá a mesma estratégia.
Mantenha o meio branco virado para você. Não há necessidade de movimentar as colunas do meio para essa resolução do cubo. Vale sempre lembrar que os meios não irão se movimentar independente dos outros movimentos no cubo. Eles permanecerão fixos na posição que estiverem, contanto que não se movimente a coluna do meio.
Lembre-se das regras explicadas anteriormente para a maioria dos cubos oficiais:
Azul sempre vai estar oposto ao Verde
Vermelho sempre vai ser oposto ao Laranja
Amarelo sempre vai estar oposto ao Branco
Isso servirá como auxílio para se localizar durante as movimentações, mas é possível resolvê-lo mesmo que essas regras estejam trocadas.
Iniciando a cruz branca:
- Comece formando uma cruz branca
- A primeira parte para montar um cubo mágico envolve fazer uma cruz na face com o meio branco. Existem algumas fórmulas para auxiliar o processo, mas é recomendável aprender a usar lógica e interpretação para movimentar as peças ao redor do cubo e montar a cruz.
- O resultado final deve ficar como as imagens abaixo. Cada lateral da cruz alinhado com o meio da outra face:
- Para o exemplo que estamos apresentando, posicione novamente o cubo com a face branca (aquela que tiver o meio da cor branca) virada para você, e a face azul (com o meio azul) virado para cima, como mostrado na imagem abaixo, e realize os movimentos:

| Oficial | Literal |
| R | Lateral Direita -> Cima |
| U | Topo -> Esquerda |
| F2 | Frente -> Direita x2 |
* Lembrando, a formula acima não faz parte do algoritmo. Serve apenas para ilustrar a montagem da cruz branca neste exemplo e permitir o leitor acompanhar a montagem. Recomenda-se o leitor usar a lógica e se acostumar com as movimentações do cubo para criar a cruz branca e preencher suas diagonais.
- Resultado final após aplicar a formula no cubo de exemplo, observa-se uma cruz branca (Neste cenário, existe uma peça posicionada errada na diagonal que eventualmente será movimentada para outro lugar do cubo) :

Preenchendo as diagonais da face branca:
- Preencher as diagonais da face branca (lembrar de colocar laterais coloridas com as respectivas faces)
- Apesar de também existirem fórmulas para ajudá-lo nesse cenário, é importante saber resolver uma face corretamente usando a lógica. Isso lhe demonstrará uma visão espacial do cubo que facilitará o aprendizado dos próximos passos.
- Lembre-se: Não tenha medo de desmontar o cubo e recomeçar tudo de novo. Se você já sabe fazer a cruz branca, poderá chegar nesse passo quantas vezes quiser.
- O resultado final deve ser algo como as imagens abaixo, a cor branca resolvida e suas laterais alinhadas com os outros meios do cubo:
- Para o exemplo que estamos apresentando, posicione novamente o cubo com a face branca (aquela que tiver o meio da cor branca) virada para você, e a face azul (com o meio azul) virado para cima, como mostrado na imagem abaixo, e realize os movimentos:

| Oficial | Literal |
| U | Topo -> Esquerda |
| B | Costas -> Esquerda |
| U’ | Topo -> Direita |
| Primeira diagonal posicionada | |
| R | Lateral Direita -> Cima |
| B | Costas -> Esquerda |
| R’ | Lateral Direita -> Baixo |
| D’ | Base -> Esquerda |
| B | Costas -> Esquerda |
| D’ | Base -> Direita |
| Segunda diagonal posicionada | |
| R | Lateral Direita -> Cima |
| B2 | Costas -> Esquerda x2 |
| R’ | Lateral Direita -> Baixo |
| Terceira diagonal posicionada | |
| D | Base -> Direita |
| B’ | Costas -> Direita |
| D’ | Base -> Esquerda |
| R’ | Lateral Direita -> Baixo |
| B’ | Costas -> Direita |
| R | Lateral Direita -> Cima |
| Todas as diagonais posicionadas com sucesso e no lugar correspondente |
* Lembrando, a formula acima não faz parte do algoritmo. Serve apenas para ilustrar a montagem das diagonais brancas neste exemplo e permitir o leitor acompanhar a montagem. Recomenda-se o leitor usar a lógica e se acostumar com as movimentações do cubo para preencher as diagonais corretamente.
** Existem formas mais otimizadas de realizar essas movimentações, mas as instruções acima abordam diferentes estratégias para encaixar as peças no lugar certo que podem ser uteis ao leitor tentando aprender a usar a lógica para montar esta etapa.
- Resultado final após aplicar a formula no cubo de exemplo, observa-se a face branca inteiramente montada com suas cores laterais alinhadas as outras faces

Preenchendo a segunda camada do cubo:
O objetivo é ter o cubo com as duas primeiras camadas completas, similar a imagem abaixo:

Tendo a face branca resolvida, posicione ela para baixo. A partir deste momento, ela se tornara a base do cubo em vez da frente.
Seguindo o exemplo que está sendo montado até agora, posicione o cubo da forma mostrada abaixo. Face branca para baixo e face amarela para cima.


O objetivo agora será construir a segunda camada.
Primeiro, encontre uma das peças que iriam para a segunda camada. No exemplo da imagem acima, a peça vermelho-verde por exemplo.

primeiramente, alinhe ela com a cor verde do cento movendo o topo.
Seguindo o embaralhamento do exemplo, a formula seria:
| Oficial | Literal |
| U’ | Topo -> Direita |
Coloque a face verde da cor selecionada a sua frente. Após mover o topo e alinhar a lateral com o centro correspondente. No caso do exemplo, escolhemos a peça verde-vermelha, ou seja, se olharmos a face verde agora após realizar o movimento, ficaria assim:

Observe que na imagem acima, a peça verde-laranja já se encontra posicionada corretamente, porém, na imagem abaixo, na mesma posição, uma peça verde se encontra no lugar incorreto onde deveria estar a peça verde-vermelha:

Observe que devemos realizar a movimentação da pela vermelho-verde para a esquerda sem desmontar o resto do cubo:


Pode ser necessário ambos os cenários. Tanto movimentar uma peça para a esquerda, quanto movimentar uma para direita, de forma a encaixa-la no lugar correto sem desmontar o progresso do cubo até o momento.
Neste cenário de exemplo, observe que do outro lado do cubo, sem realizar nenhum movimento ainda, uma peça precisa ser movimentada para a direita. A peça vermelho-azul:

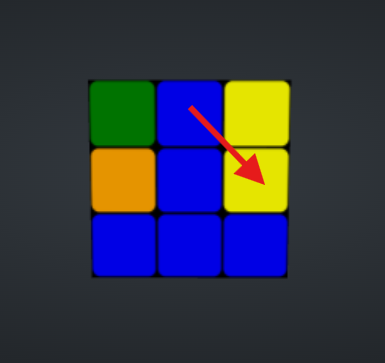
A seguir, as formulas para movimentar para a direita ou esquerda conforme a necessidade (Essas são formulas oficiais, aplicáveis para qualquer embaralhamento, de forma a mover as laterais sem bagunçar as outras camadas do cubo):
Movimentar lateral para a esquerda:
Olhe para a face que deseja movimentar e realize a formula:
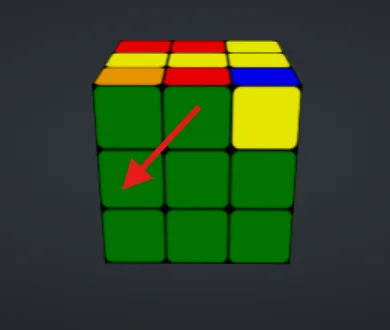
| Oficial | Literal |
| U’ | Topo -> Direita |
| L’ | Lateral Esquerda -> Cima |
| U | Topo -> Esquerda |
| L | Lateral Esquerda -> Baixo |
| U | Topo -> Esquerda |
| F | Frente-> Direita |
| U’ | Topo->Direita |
| F’ | Frente->Esquerda |
Resultado após formula, a peça está posicionada no local correto, sem atrapalhar as outras duas camadas já feitas:

Observe que o topo (face amarela no caso), ficou embaralhado e não manteve a mesma posição de antes. Isso é normal.
Se necessário, movimente o topo novamente para esquerda ou direita para alinhar outra peça novamente.
No caso do exemplo,
| Oficial | Literal |
| U | Topo -> Esquerda |
Ao girar o cubo, vai voltar em uma posição parecida ao que estava antes:

Agora será necessário movimentar para a direita.

Movimentar lateral para a direita:


| Oficial | Literal |
| U | Topo -> Esquerda |
| R | Lateral Direita -> Cima |
| U’ | Topo -> Direita |
| R’ | Lateral Direita -> Baixo |
| U’ | Topo -> Direita |
| F’ | Frente -> Esquerda |
| U | Topo -> Esquerda |
| F | Frente -> Direita |
A formula acima também é parte do método para resolver o cubo. Segue resultado ao finalizar:

É possível que a peça saia no local certo, mas na posição incorreta. Como mostrado no mesmo cubo, sem realizar nenhum movimento ainda.

Quando isso ocorrer, é necessário retirar a peça e recoloca-la no lugar.
A seguir, a forma como fazer isso no exemplo mostrado. Basicamente, será utilizado a formula de ‘Movimentar lateral para esquerda’ :

| Oficial | Literal |
| U’ | Topo -> Direita |
| L’ | Lateral Esquerda -> Cima |
| U | Topo -> Esquerda |
| L | Lateral Esquerda -> Baixo |
| U | Topo -> Esquerda |
| F | Frente-> Direita |
| U’ | Topo->Direita |
| F’ | Frente->Esquerda |

Agora, é necessário alinhar novamente a cor da peça que precisa ser ajustada com a face correspondente.
No exemplo que estamos utilizando, realize a movimentação para alinhar a peça:
| Oficial | Literal |
| U2 | Topo -> Esquerda x2 |

Em seguida, realizar a formula de movimentar lateral para a esquerda novamente:
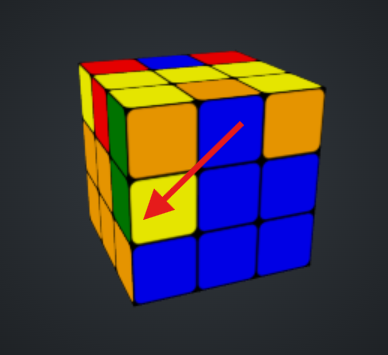
| Oficial | Literal |
| U’ | Topo -> Direita |
| L’ | Lateral Esquerda -> Cima |
| U | Topo -> Esquerda |
| L | Lateral Esquerda -> Baixo |
| U | Topo -> Esquerda |
| F | Frente-> Direita |
| U’ | Topo->Direita |
| F’ | Frente->Esquerda |
Resultado após realizar a fórmula acima. Vale ressaltar que é a mesma utilizada antes para movimentar a lateral desejada do topo para a esquerda.

Agora devemos criar uma cruz amarela no topo, seguindo as fórmulas necessárias.
Montar Cruz Amarela:
Ao resolver as duas primeiras camadas, o topo do cubo pode estar em 4 formas diferentes.
Ignorando as peças que não fazem parte da cruz amarela, o topo pode estar:
(imagens retiradas do site https://jperm.net/3×3)
- Cenário 1: Apenas uma peça da cruz no centro
- Cenário 2: Três peças da cruz montadas, formando uma imagem parecida com uma seta
- Cenário 3: Três peças da cruz montadas, formando uma linha:
- Cenário 4: Cinco peças já montadas, com a cruz amarela completa:
Formula para montar a cruz amarela com base nos cenários acima (Exceto cenário 4, visto que a cruz já se encontra completa:
No caso do cenário 1, 2 ou 3, pode ser necessário realizar a formula mais de uma vez, pois uma posição pode se transformar em outra.
No caso do cenário 2, posicionar a “seta” invertida apontada para a esquerda e realize formula abaixo.

No caso do cenário 3, posicionar linha horizontal a sua visão e realizar a formula abaixo.

No caso do exemplo que estamos seguindo para o artigo, observa-se o cenário 3:
Posicione a linha amarela na sua horizontal. Para o exemplo, estaremos olhando para a face vermelha


E realize a formula para montar a cruz amarela:
| Oficial | Literal |
| F | Frente -> Direita |
| R | Lateral Direita -> Cima |
| U | Topo -> Esquerda |
| R’ | Lateral Direita -> Baixo |
| U’ | Topo -> Direita |
| F’ | Frente-> Esquerda |
Resultado após a realização da fórmula

Como mencionado anteriormente, pode ocorrer ao realizar a fórmula da cruz amarela de chegar em outros cenários (2 ou 3)
No cenário 2, posicione a “seta invertida” a sua esquerda para realizar a formula. No cenário 3, visualize a linha de forma horizontal e realize a formula. Normalmente duas vezes são o máximo necessário para realizar a cruz amarela, independente do cenário.
Para o exemplo utilizado, as cores ficaram alinhadas corretamente com cada face.
Ao realizar a movimentação
| Oficial | Literal |
| U | Topo -> esquerda |
Cada cor da cruz amarela fica alinhada com sua face. Isso não ocorre normalmente, sendo necessário uma formula para ajustar os cantos da cruz amarela com as faces correspondentes, o ocorrido foi apenas uma condição de sorte do cubo.

A formula oficial que seria realizada para ajustar os cantos da cruz amarela (que não deve ser realizada no exemplo, visto que já veio pronto no cubo) seria:
Ajustar cantos cruz amarela
Tente alinhar Apenas uma das faces do topo com a cor correspondente, mesmo que as outras não estejam alinhadas. Como demonstrado na imagem abaixo.

Se houverem mais cores alinhadas, é necessário movimentar o topo e realizar a formula olhando para a face com a única cor correta. Se não houver forma de deixar apenas uma correta, alinhe do mesmo jeito e realize a formula mais de uma vez (não realize a formula se estiver seguindo o exemplo do artigo).
| Oficial | Literal |
| R | Lateral Direita -> Cima |
| U | Topo -> Esquerda |
| R’ | Lateral Direita -> Baixo |
| U | Topo -> Esquerda |
| R | Lateral Direita -> Cima |
| U2 | Topo -> Esquerda x2 |
| R’ | Lateral Direita -> Baixo |
Conforme a prática da formula, é possível identificar posições em que seria melhor utiliza-la, mas que não serão abordadas neste artigo para fins de praticidade.
Posicionar diagonais da face amarela:
Após a cruz amarela estar completa, é necessário posicionar as diagonais do cubo nos lugares correspondentes.
Realize a formula seguindo a imagem do exemplo abaixo:

Posicione a diagonal que estiver certa a sua direita, como na imagem abaixo. Observa-se que a diagonal Laranja-Azul-Amarelo se encontra no lugar que deveria, necessitando alterar a posição das outras.
É possível chegar em cenários que nenhuma delas esteja no local certo. Se for o caso, realize a formula com qualquer uma delas a sua direita.
No caso do exemplo abordado neste artigo, posicione o cubo desta maneira, com a diagonal certa a sua direita, e realize a formula olhando para a face verde.

Realizar a formula:
| Oficial | Literal |
| L | Lateral esquerda -> Baixo |
| U’ | Topo -> Direita |
| R’ | Lateral Direita -> Baixo |
| U | Topo -> Esquerda |
| L’ | Lateral Esquerda -> Cima |
| U’ | Topo -> Direita |
| R | Lateral Direita -> Cima |
| U | Topo -> Esquerda |
Observa-se que o cenário encontrado também é uma situação incomum, onde as duas ultimas peças a serem resolvidas estão em diagonais opostas:

Normalmente o cubo não se encontra nesta maneira, mas o formato de resolução apresentado abaixo poderá resolver tanto este formato quanto os formatos mais comuns.
A formula abaixo servirá para orientar as duas cores das laterais, movimentando-as para a direita.
Coloque a face vermelha a sua frente, o movimento a ser realizado irá orientar as duas laterais para os lados opostos, como demonstrado na imagem:

A peça Verde-Amarela-Vermelha ficará correta, porém a Amarela-Vermelha-Azul será danificada, porém será arrumada na próxima formula.
Realize a formula abaixo, no caso do exemplo, olhando para a face vermelha:
Orientando Diagonais finais da face amarela
| Oficial | Literal |
| Parte 1 | |
| F | Frente -> Direita |
| D | Base -> Direita |
| F’ | Frente -> Esquerda |
| D’ | Base -> Esquerda |
| F | Frente -> Direita |
| D | Base -> Direita |
| F’ | Frente -> Esquerda |
| Parte 2 | |
| U’ | Topo -> Direita |
| F | Frente -> Direita |
| D’ | Base -> Esquerda |
| F’ | Frente -> Esquerda |
| D | Base -> Direita |
| F | Frente -> Direita |
| D’ | Base -> Esquerda |
| F’ | Frente -> Esquerda |
| U | Topo -> Esquerda |
Resultando na imagem abaixo:

Em seguida, realize a formula novamente olhando para a face azul:

| Oficial | Literal |
| Parte 1 | |
| F | Frente -> Direita |
| D | Base -> Direita |
| F’ | Frente -> Esquerda |
| D’ | Base -> Esquerda |
| F | Frente -> Direita |
| D | Base -> Direita |
| F’ | Frente -> Esquerda |
| Parte 2 | |
| U’ | Topo -> Direita |
| F | Frente -> Direita |
| D’ | Base -> Esquerda |
| F’ | Frente -> Esquerda |
| D | Base -> Direita |
| F | Frente -> Direita |
| D’ | Base -> Esquerda |
| F’ | Frente -> Esquerda |
| U | Topo -> Esquerda |

Um cubo montado com sucesso.
OBS:
Existem diversas simplificações que podem ser realizadas para diminuir o número de movimentos na resolução do cubo, incluindo pular certas etapas. Recomenda-se ao leitor buscar novas formas de cortar caminhos.
Este artigo focou principalmente em abordar uma forma de resolução prática, apresentando as principais formulas de resolução do método adaptado Fridrich/CFOP + alguns cenários incomuns que poderiam aparecer ao longo da montagem.
Lembre-se, não tenha medo de errar e perder todo o seu progresso ao montar um cubo. Se você já sabe chegar onde está, basta apenas aprender com seus erros e voltar ao mesmo lugar.
Fontes:
https://en.wikipedia.org/wiki/CFOP_method
https://pt.wikipedia.org/wiki/Jessica_Fridrich
https://www.youtube.com/watch?v=Qhx8pKyxCrM
https://www.youtube.com/watch?v=SRGxSi8Wfn0
Rafael Lua, formado em Ciência da Computação. Curioso por natureza, sempre buscando novas formas de entender o mundo e se divertir no processo.